Asymmetric Cryptography
Xiphera’s offering for Asymmetric Cryptography includes solutions for key exchange, digital signatures, and public-key encryption.
Asymmetric cryptography, also known as public-key cryptography, is a fundamental concept in the field of information security. It’s a cryptographic technique that uses a pair of mathematically related keys (a public key and a private key) to perform two main functions: key exchange and digital signatures.
The most famous asymmetric cryptographic approach is the RSA (Rivest-Shamir-Adleman) algorithm, but the current state-of-the-art asymmetric cryptography is based on elliptic curves mathematics, which are complicated mathematical algorithms combining security with efficient computations and small key sizes. Elliptic Curve Cryptography (ECC) commonly uses standardised elliptic curves such as the NIST curves by the U.S. National Institute of Standards and Technology (NIST) or the newer Curve25519.
Xiphera offers a broad spectrum of the above-mentioned modern and widely used asymmetric cryptography:
- ECC Accelerator
- Elliptic Curve Diffie-Hellman (ECDH) and Elliptic Curve Digital Signature Algorithm (ECDSA) on NIST prime curves
- Curve25519 – public-key exchange and digital signatures
- RSA signature verification
Our Asymmetric Cryptography offering is developed according to the needs of our customers and optimised for performance and resource usage. Our implementations are device-agnostic and can support all FPGA (Field Programmable Gate Arrays) and ASIC (Application Specific Integrated Circuits) technologies available in the market.
Asymmetric cryptography uses two separate keys to encrypt. These keys are known as a ‘Public Key’ and a ‘Private Key.’ Private and public keys are related so that a public key can be derived from a private key, but recovering the private key from the public key is infeasible. As the names hint, public keys can be publicly distributed, but private keys must be stored securely. Public keys permit anybody to do certain operations like encrypt data, whereas certain other operations like decryption can be done only with the private key.
Hybrid models connect classical security and quantum-secure cryptography
Modern day public-key cryptography is largely covered by RSA and ECC. With quantum technology advancing every year, these classical asymmetric cryptographic algorithms will be vulnerable to attacks by advanced quantum computers and their computational power. Although powerful enough quantum computers are not known to yet exist, this threat needs to be prepared for already today.
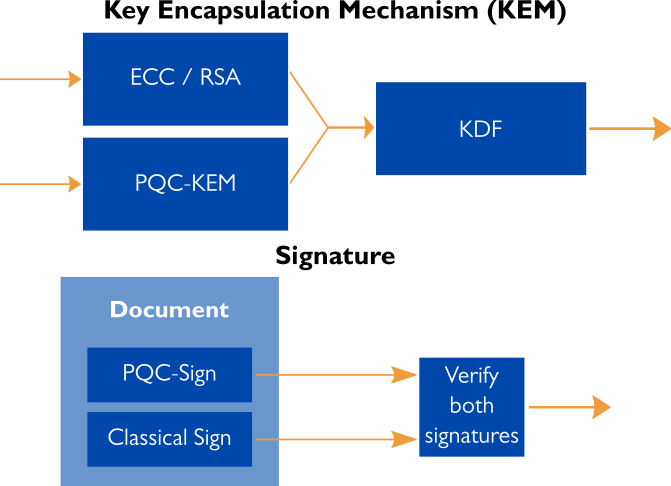
The current recommendation (for instance by the National Cybersecurity Agency of France ANSSI) is to use a hybrid model, where the Post-Quantum Cryptographic (PQC) algorithm is used in combination with a classical cryptographic algorithm (for example, RSA or ECC). When faced with a quantum adversary breaking classical algorithms, the hybrid system remains secure due to the PQC component. If some unknown exploit of the new PQC algorithms were to arise, the tried-and-true classical component of the hybrid system would hold steady. We at Xiphera help our customers to implement the hybrid security model by combining our in-house Asymmetric Cryptography solutions with our xQlave® PQC solutions.
Use cases
Asymmetric cryptography is commonly used for securing communication channels (e.g., via SSL/TLS), digital signatures for document verification, and secure email communication (PGP/GPG). The main use cases of asymmetric cryptography in contemporary secure communication protocols are:
- Key exchange, allowing two parties to securely derive a shared secret key (for example, for bulk data encryption by AES) over an insecure channel.
- Digital signatures, enabling signing messages with a private key so that anyone can later verify the signature with the public key in order to get assured that the message was indeed signed by claimed signer. Digital signatures form the basis of certificate-based public-key infrastructure (PKI) that brings trust into the modern Internet (e.g., in the HTTPS protocol).
- Public-key encryption, encrypting data using a party’s public key so that only that party (the holder of the corresponding private key) can decrypt the data.
